I am a researcher in applied mathematics at the Modelling group of ESILV Paris-Nantes.
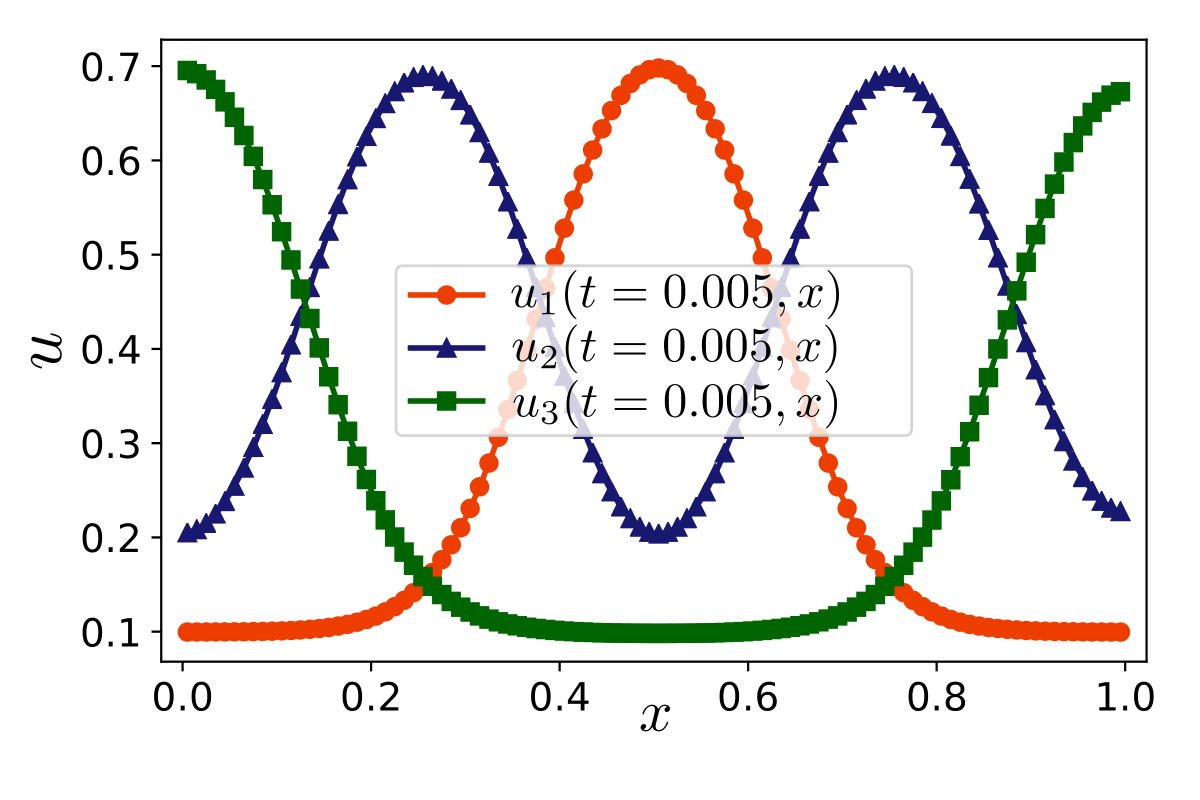
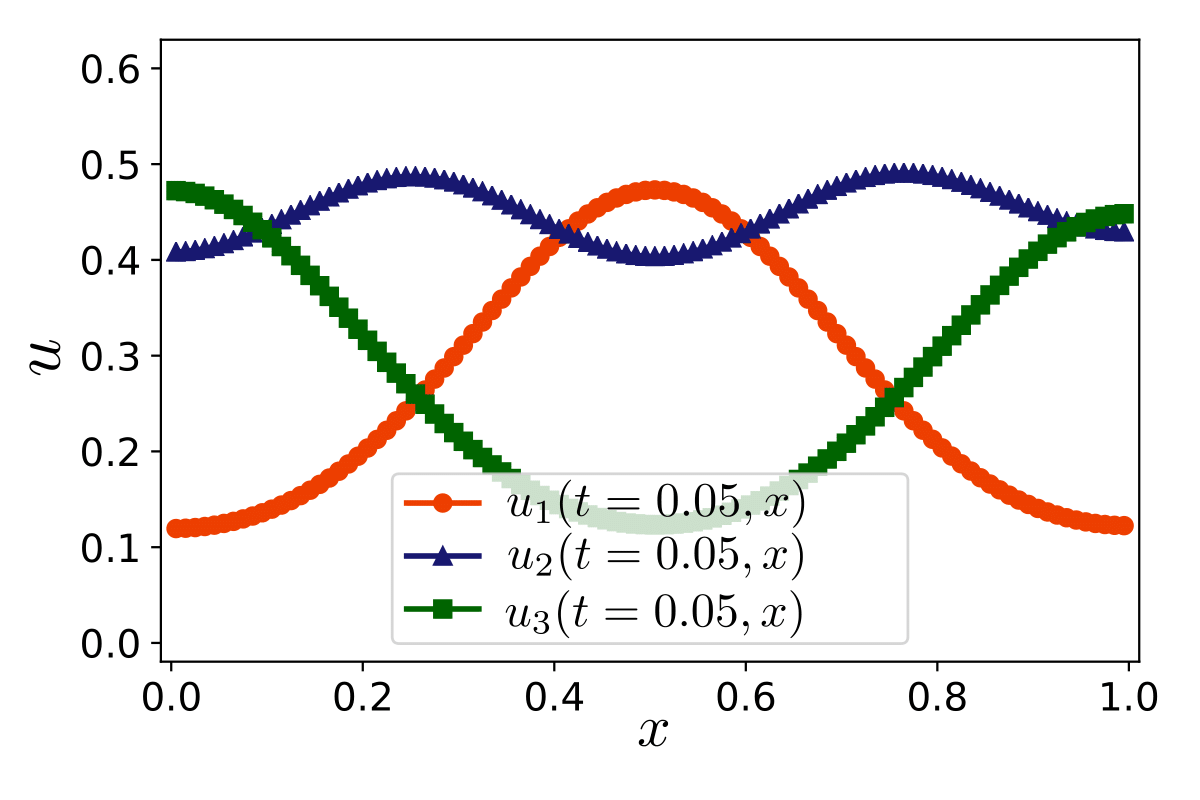
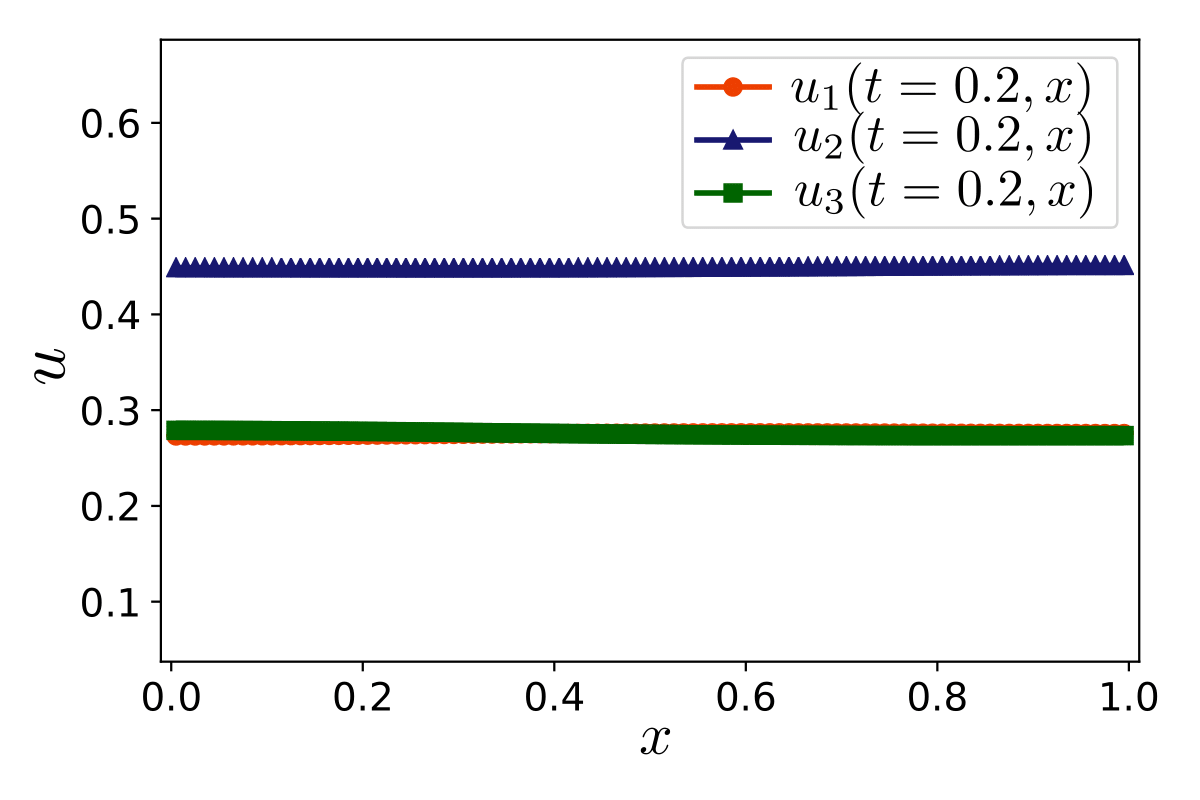
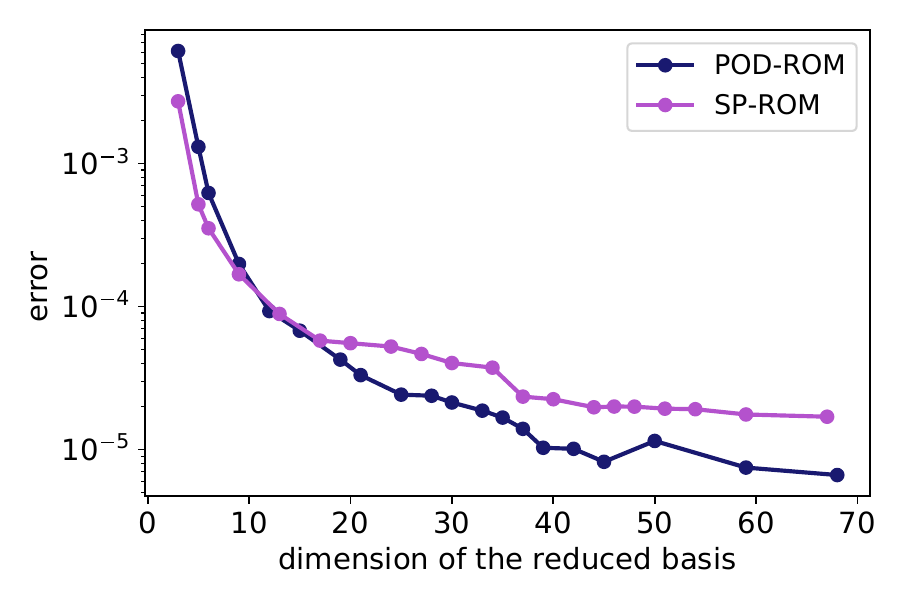
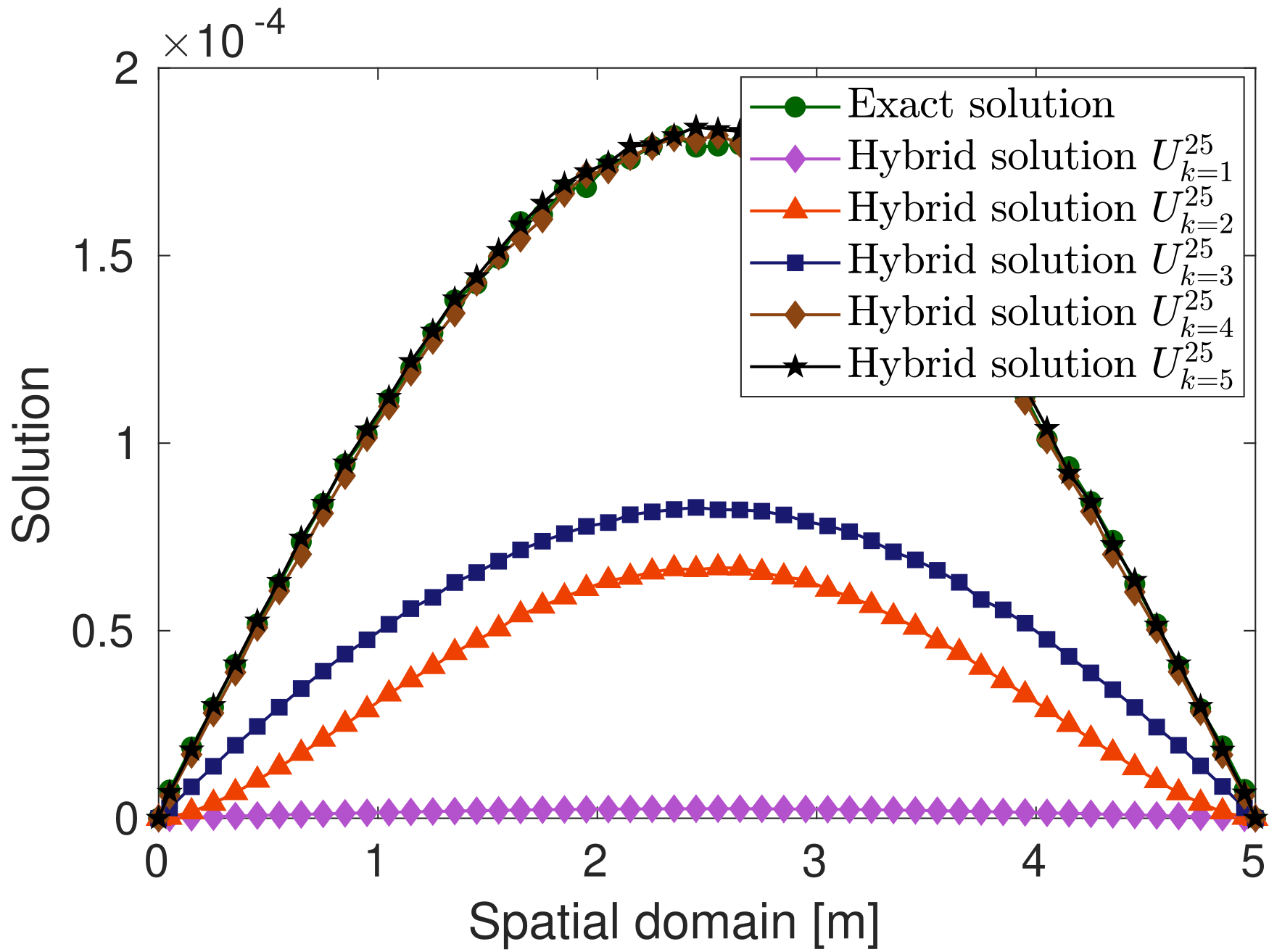
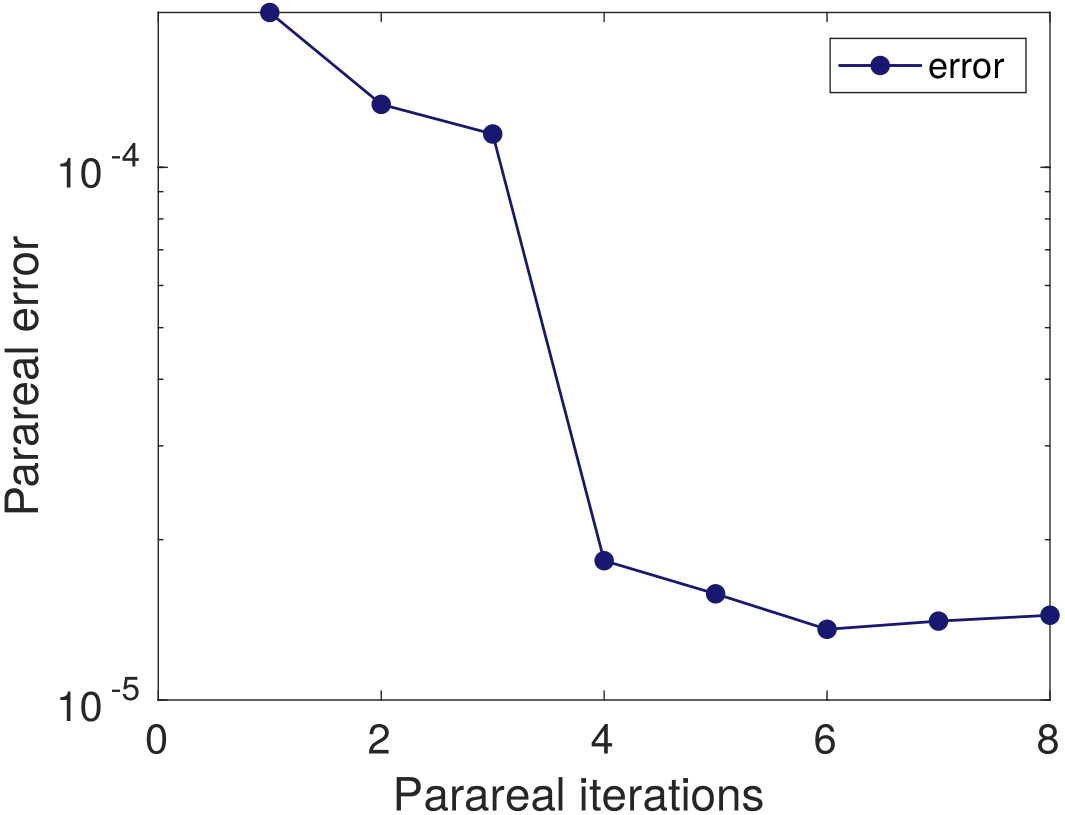
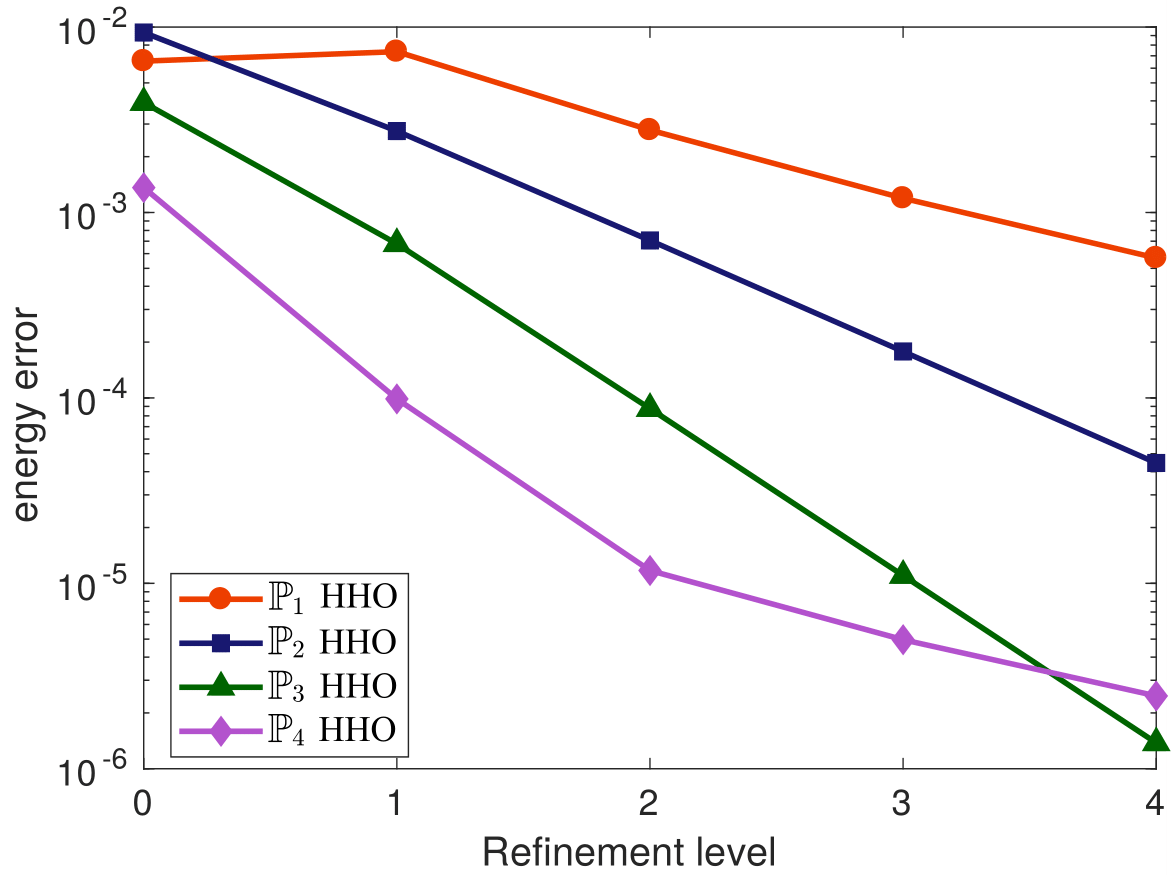
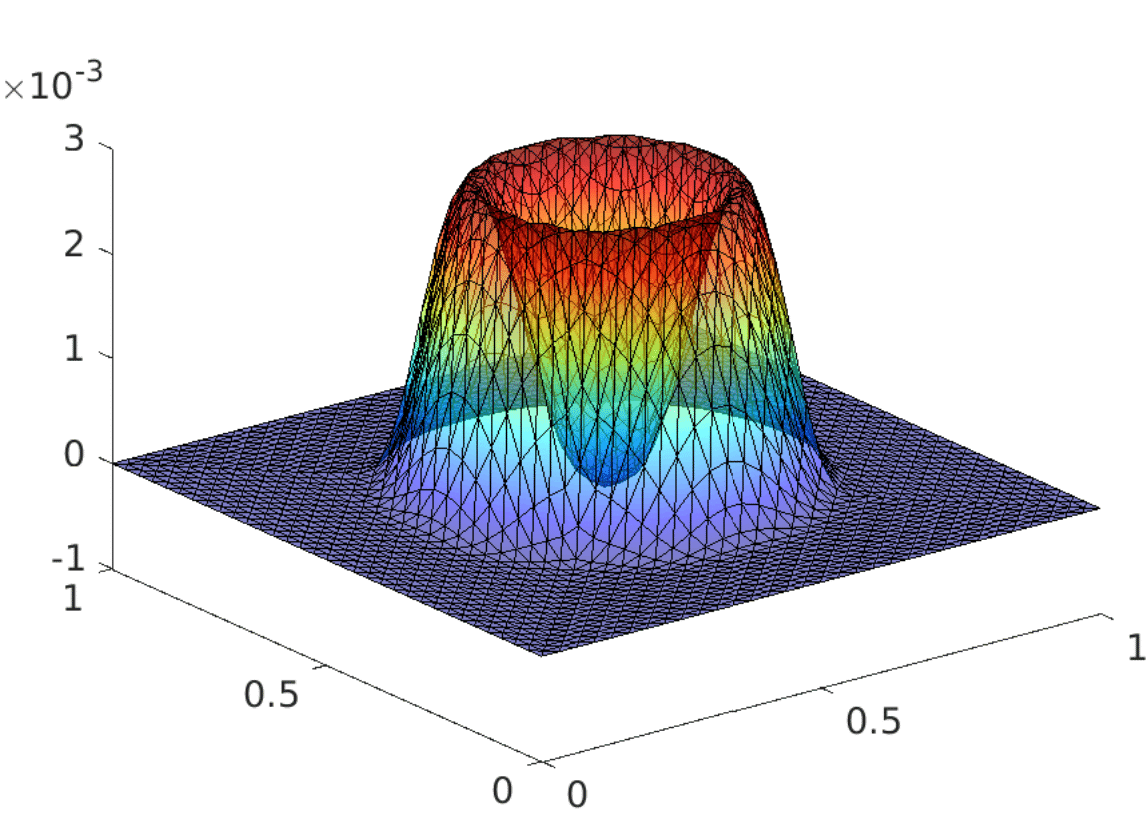
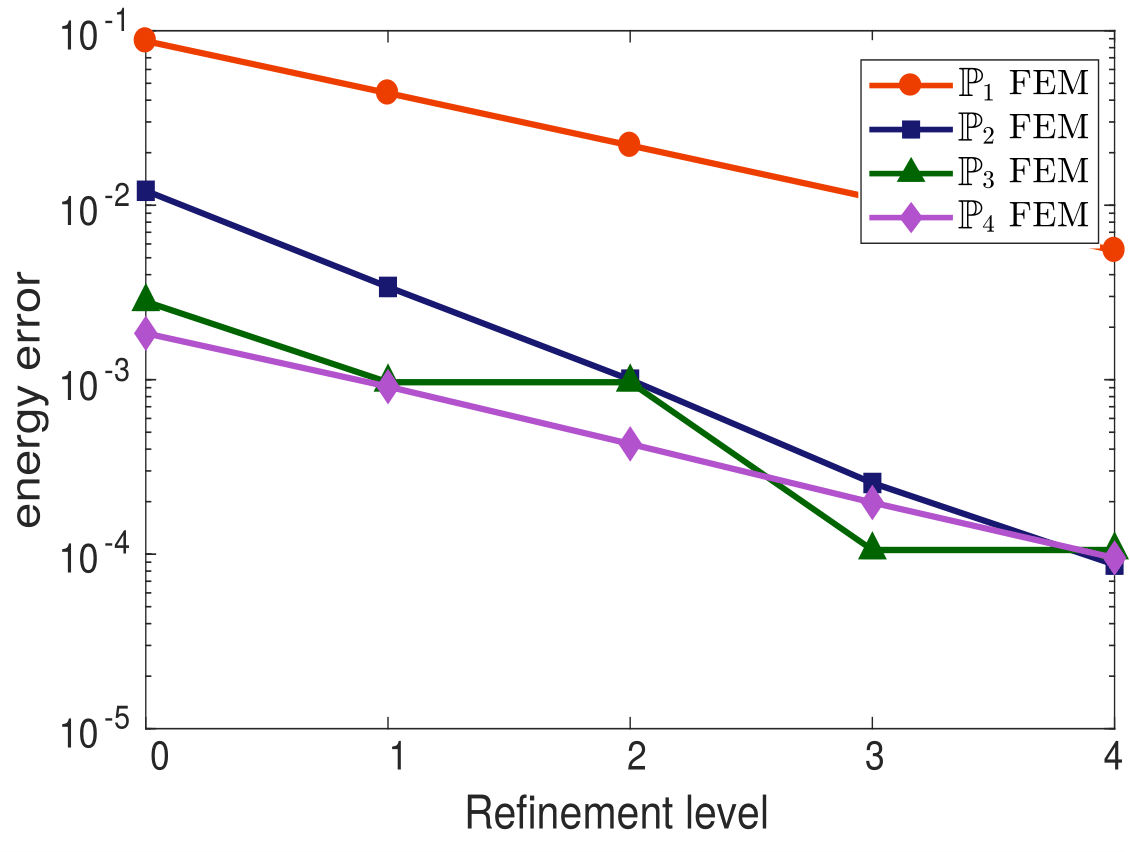
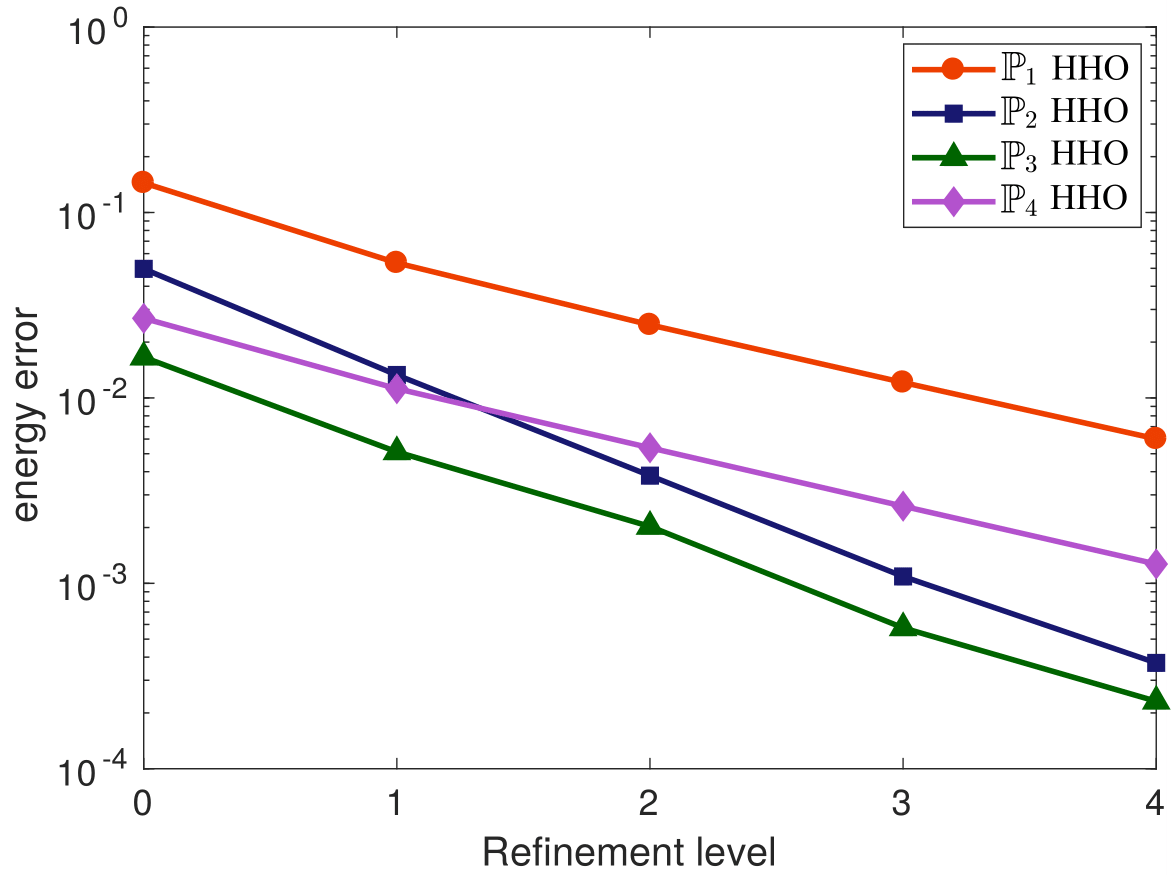
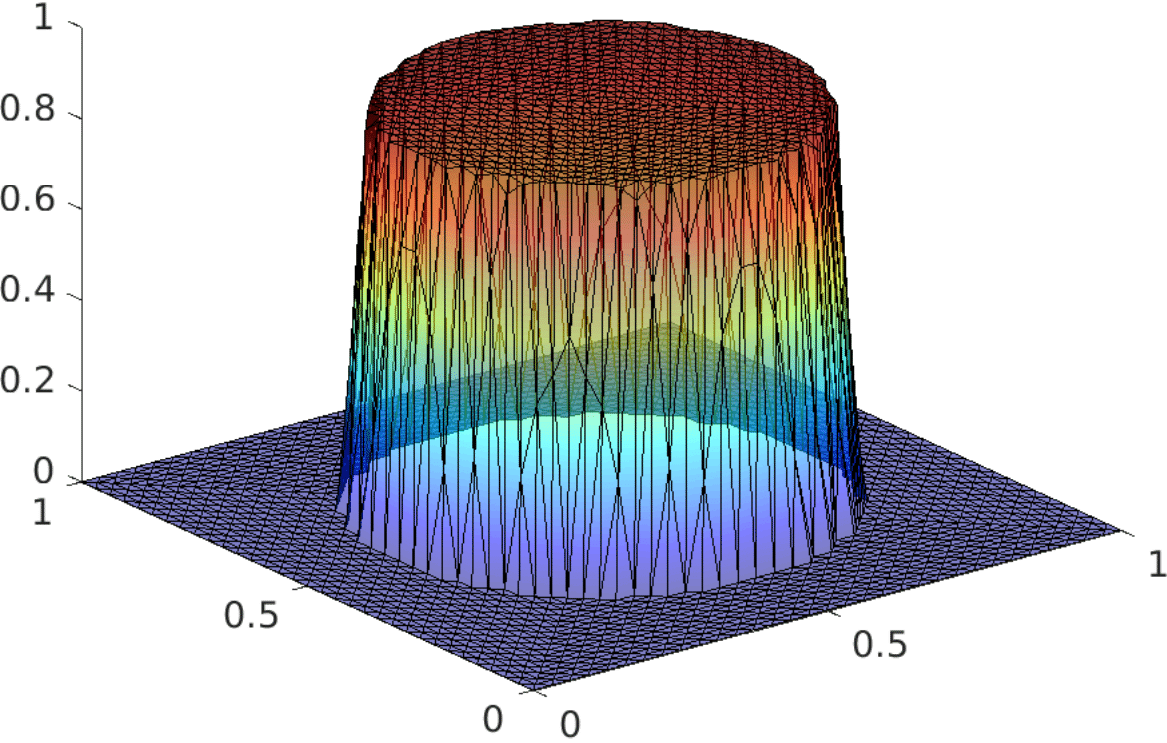
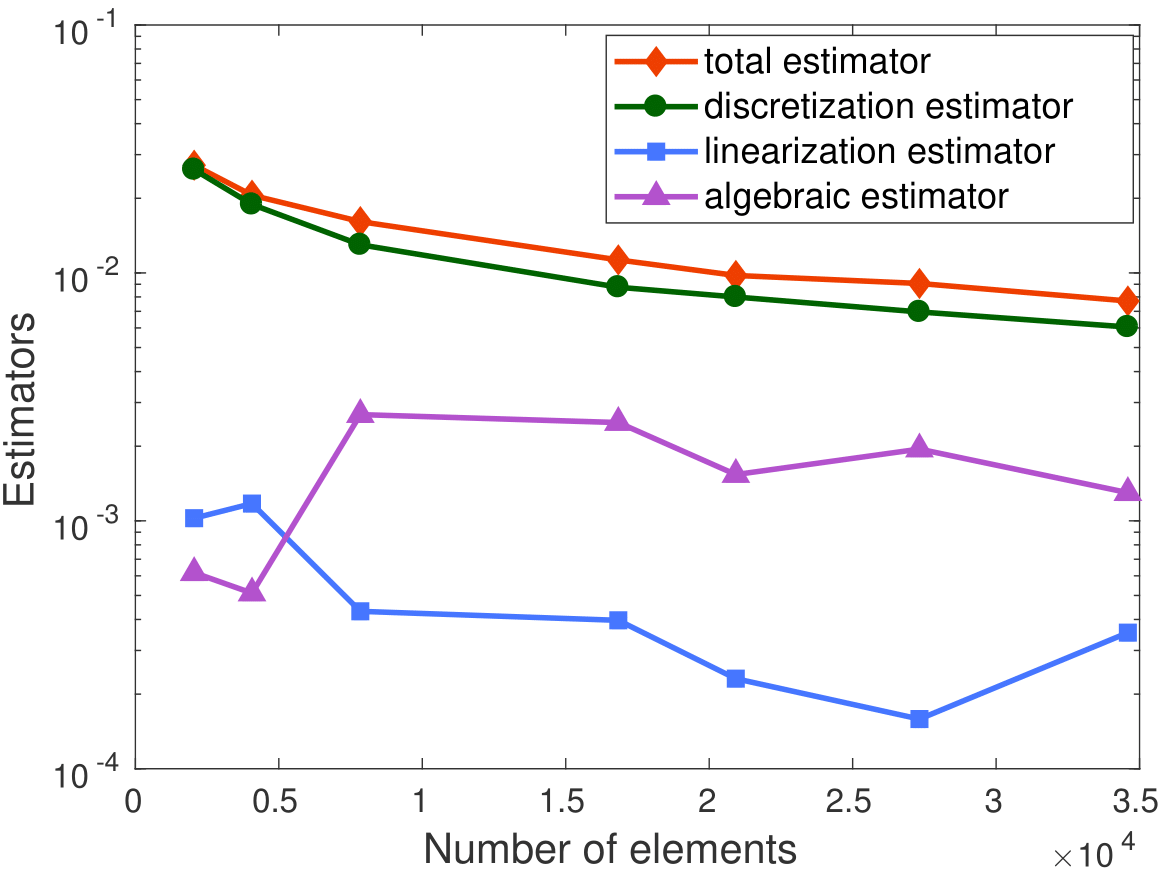
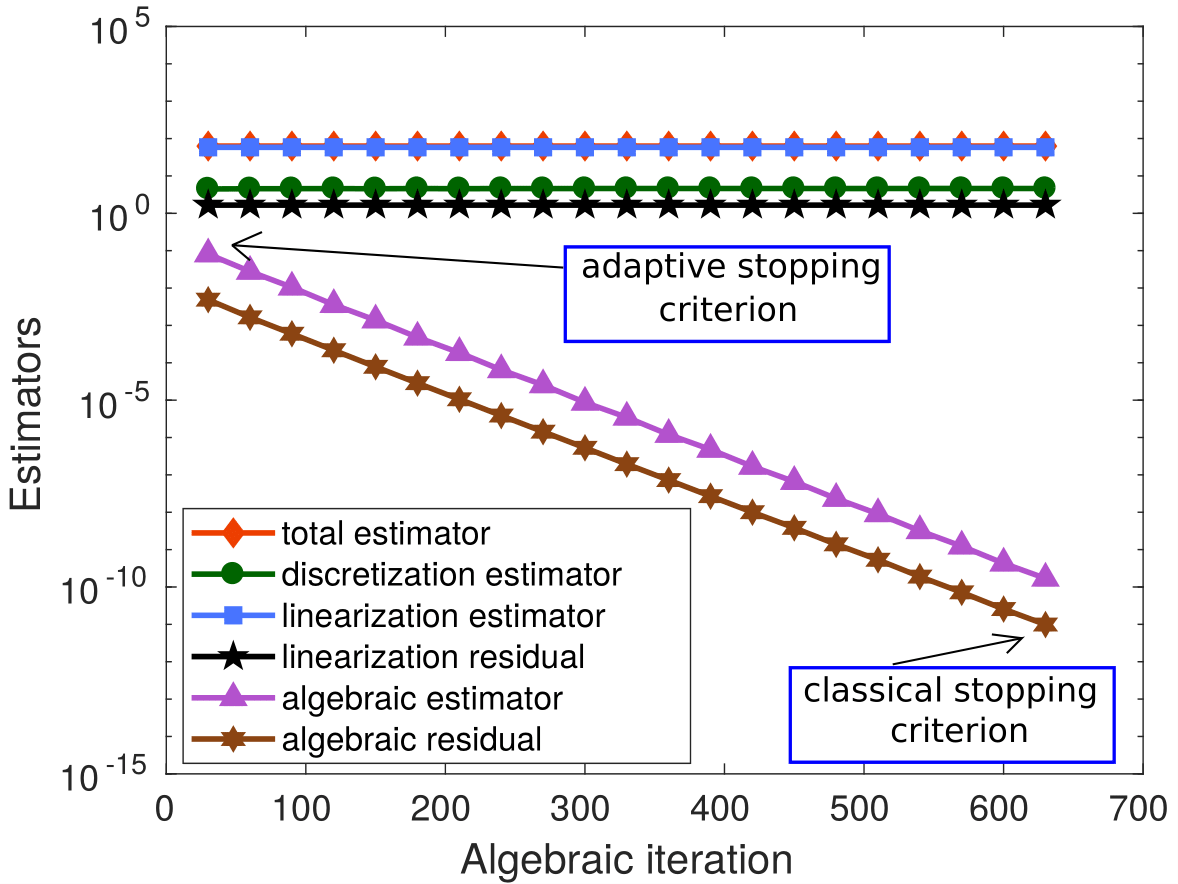
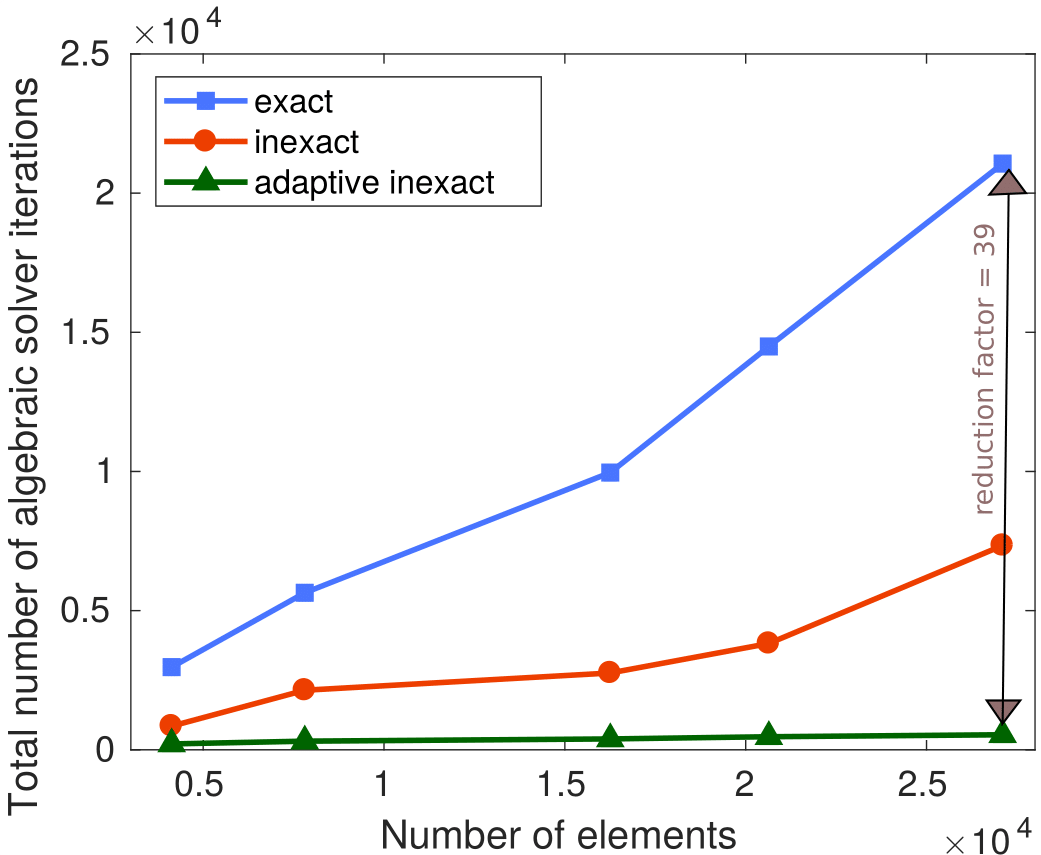
My research activity mainly focus on the mathematical and numerical analysis of partial differential equations arising in environmental and biology processes.
April 2021- August 2022 : Postdoctoral position at Ecole des Ponts ParisTech, CERMICS, supervised by Virginie Ehrlacher . This postdoctoral program was supported by the ANR project COMODO .
In this postdoctoral position, I developped a structure preserving reduced order model for the resolution of cross-diffusion systems.
The goal is to treat the cross-diffusion system arising within the PVD process dedicated to the fabrication of solar cells.
September 2019 - February 2021 : Postdoctoral position at CEA Paris-Saclay & Sorbonne Université, supervised by
Andrea Zoia and Yvon Maday .
This postdoctoral program was supported by the ANR project Ciné-Para .
In this postdoctoral position, I developped a hybrid parareal algorithm for parabolic problems and for the kinetic neutron transport problem. The goal was to speed up a Monte-Carlo resolution for time-dependent problems using a parallel-in-time approach.
In this PhD thesis, I derived a posteriori error estimates including adaptive stopping criteria for variational inequalities. I studied problems in contact mechanics and a multiphase multicomponent flow in porous media describing the storage of radioactive wastes in deep geological layers.
Variational inequalities (contact mechanics, multiphase flow in porous media)
Parallel-in-time methods, reduced basis methods
Random process (Monte Carlo methods, diffusion equation, neutronic)
Optimisation
Some numerical results
Some results on cross-diffusion systems
In the first three images is represented the evolution of the concentrations of 3 species as a function of time. The concentrations evolve to constant profiles. In the last image is plotted the behavior of two reduced order model error. A standard POD error and a structure preserving SP error.
Some results on a parareal-in-time resolution for speeding a Monte Carlo resolution dedicated to the heat equation.
In the following images is represented a parareal resolution for the heat equation. In the parareal resolution, the coarse propagator is the finite element solver and the fine propagator is the Monte Carlo solver. Few parareal iterations are needed to speed up the resolution.
Some results for high order discretizations of variational inequalities
In the following images, is represented the error in the energy norm for a smooth solution (not realistic case) and compare the finite element method and the HHO method.
In the following images, is represented the error in the energy norm for a realistic solution (discontinuous Lagrange multiplier) and compare the finite element method and the HHO method.
In the following images, is represented the concept of adaptivity for inexact semismooth Newton resolutions of variational inequalities.
The first image shows the overall behavior of the estimators as a function of the number of mesh elements. For exact and inexact semismooth Newton resolutions the discretization estimator is dominant and the linearization and algebraic estimators are small. In the adaptive inexact semismooth Newton resolution, the linearization and algebraic estimators are sufficiently small to not influence the behavior of the discretization estimator.
The second image focuses on the behavior of the different error estimators as a function of the linear algebra (GMRES) resolution. An important number of algebraic iterations can be saved. The third image shows the overall performance of three methods.
Scientific stays
IMAG: invited by Prof Daniele Di Pietro , University of Montpellier, November 2021, France.
CEMRACS, July-August 2021, Luminy, France.
Research project: Computation of the auto-diffusion coefficient for a cross diffusion problem with tensor methods.
In collaboration with Virginie Ehrlacher and Christoph Strossner
